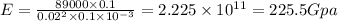Answer:
222.5 Gpa
Step-by-step explanation:
From definition of engineering stress,
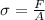
where F is applied force and A is original area
Also, engineering strain,
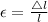 where l is original area and
where l is original area and
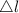 is elongation
is elongation
We also know that Hooke's law states that
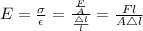
Since A=20 mm* 20 mm= 0.02 m*0.02 m
F= 89000 N
l= 100 mm= 0.1 m
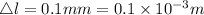
By substitution we obtain