Answer:
a) v = 3 10⁶ m / s , b) a = 1.055 10¹² m / s² , c) r = 8.53 m
Step-by-step explanation:
a) Let's use Newton's Second Law of Balance, so that electrons do not deviate
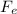 -
-
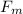 = 0
= 0
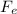 =
=
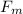
q E = q v B
v = E / B
Let's calculate
v = 6.0 10³ / 2.0 10⁻³
v = 3 10⁶ m / s
b) If the electric field is disconnected, the only force left is the magnetic one
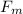 = m a
= m a
q v B = m a
a = q / m v B
a = q / m (E / B) B
a = q / m E
a = 1.6 10⁻¹⁹ /9.1 10⁻³¹ 6.0 10³
a = 1.055 10¹² m / s²
c) Acceleration is centripetal
a = v² / r
r = v² / a
r = (3 10⁶)² /1.055 10¹²
r = 8.53 m