Question

In a classic carnival ride, patrons stand against the wall in a cylindrically shaped room. Once the room gets spinning fast enough, the floor drops from the bottom of the room! Friction between the walls of the room and the people on the ride make them the "stick" to the wall so they do not slide down. In one ride, the radius of the cylindrical room is R = 6.1 m and the room spins with a frequency of 21.7 revolutions per minute. What is the speed of a person "stuck" to the wall? What is the normal force of the wall on a rider of m = 53.0 kg?

Answer 1

13.86175 m/s

1669.4836 N

Step-by-step explanation:

`\omega` = Angular frequency =
`(2\pi* 21.7)/(60)\ rad/s`

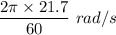
r = Radius = 6.1 m

m = Mass of person = 53 kg

Angular speed of the person is given by

`v=\omega r\\\Rightarrow v=2\pi fr\\\Rightarrow v=2\pi (21.7)/(60)* 6.1\\\Rightarrow v=13.86175\ m/s`

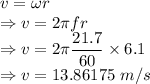
Speed of a person "stuck" to the wall is 13.86175 m/s

Normal force is given by

`F=(mv^2)/(r)\\\Rightarrow F=(53* 13.86175^2)/(6.1)\\\Rightarrow F=1669.4836\ N`

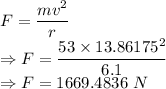
The normal force of the wall on the rider is 1669.4836 N