Question

assuming ideal behavior, calculate the boiling point in C of solution that contains 64.5g or the non-volatile non-electrolyte quinoline( molar mass= 129g/mole) in 500 grams of benzene. For benzene the normal boling point is 80.10 C and Kb = 2.53C/m

Answer 1

Step-by-step explanation:

The given data is as follows.

mass of solute = 64.5 g, mass of solvent = 500 g = 0.5 kg (as 1 kg = 1000 g),

Temperature =
`80.10^(o)C`,
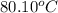`K_(b)` = 2.53 C/m

Also, we know that the relation between change in temperature, van't Hoff factor(i) and
`K_(b)` is as follows.

`\Delta T = iK_(b)m`

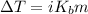
where, m = molality =
`\frac{\text{moles of solute}}{\text{kg of solvent}}`

=
`(64.5 g)/(129 g/mol) * (1)/(0.5 kg)`

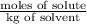
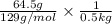
= 1

It is known that for non-electrolyte solute i = 1.

Hence, putting the given values into the above formula as follows.

`\Delta T = iK_(b)m`

=
`1 * 2.53 C/m * 1`

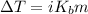
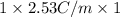
= 2.53 C

Therefore, calculate the boiling point of the solution as follows.

80.10 C + 2.53 C

= 82.63 C

Thus, we can conclude that the boiling point of the solution is 82.63 C.