To solve this problem we will use Snell's law. This law is used to calculate the angle of refraction of light by crossing the separation surface between two means of propagation of light (or any electromagnetic wave) with a different index of refraction.
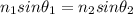
Where,
 = Index of refraction for each material
= Index of refraction for each material
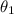 = Angle of incidence and refraction
= Angle of incidence and refraction
A ray of light propagating in a medium with index of refraction
 hitting an angle
hitting an angle
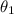 on the surface of a medium of index
on the surface of a medium of index
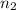 with
with
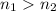 can be fully reflected inside the medium of highest refractive index:
can be fully reflected inside the medium of highest refractive index:
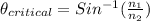
 Refractive index of rarer medium
Refractive index of rarer medium
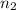 Refractive index of denser medium
Refractive index of denser medium
Replacing we have,
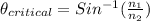
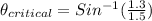
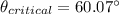
the critical angle of this fiber at the glass-plastic interface is 60.07°