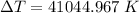Answer:
The temperature of air will increase by
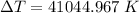
Step-by-step explanation:
Given:
- no. of person in a theater,
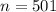
- volume of air in the theater,
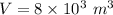
- rate of heat given off by each person,
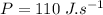
- duration of movie,
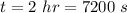
- initial pressure in the theater,
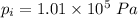
- initial temperature in the theater,
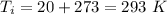
- specific heat capacity of air at the given conditions,
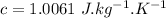
The total quantity of heat released by the total people in the theater during the movie:
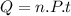
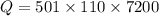
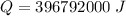
Form the relation of heat capacity:
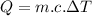
∵
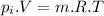

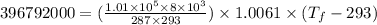

Change in temperature of air: