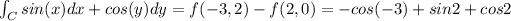Question

Evaluate the line integral, where C is the given curve. ∫C sin(x) dx + cos(y) dy, where C consists of the top half of the circle x^2 + y^2 = 4 from (2, 0) to (−2, 0) and the line segment from (−2, 0) to (−3, 2)

Answer 1

`\int_C sin(x) dx - cos(y) dy=f(-3,2)-f(2,0)= -cos(-3) +sin 2 + cos 2`

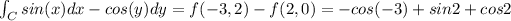
Explanation:

Previous concepts

Fundamental Theorem of Line Integrals and into Green’s Theorem

Suppose a Curve C given by the vector function
`r(t)` with a= r(a) and b= r(b). Then we have this:

`\int_C V f . dr = f(b)-f(a)`

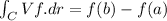
Where Vf represnent the gradient of the function f.

Solution to the problem

We want to find this integral:

`\int_C sin(x) dx + cos(y) dy`

And the region C is given by the top half circle with equation
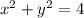`x^2 + y^2 = 4` with radius 2 and we have a line segment from (-2,0) to (-3,2).

In order to solve this problem we can use this form:

`\int_C P(x,y) dx +\int_C P(x,y) dy = \textbf{F(r(t))} . dr`

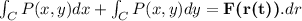
Where
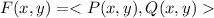`F(x,y) =<P(x,y),Q(x,y)>` is a bivariate function.

For our case our function F is given by:
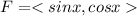`F=<sin x, cos x>` and that represent our vector field.

We can find the potential function or the antiderivate like this:

`f(x,y) = -cos x + sin y`

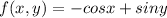
At the point (2,0) we can find the potential function and we got:

`f(2,0) = -cos 2 + sin 0 = -cos 2`

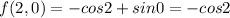
At the point (-3,2) we can find the potential function and we got:

`f(-3,2) = -cos (-3) + sin 2 = -cos (-3) +sin 2`

And then the integral is given by:

`\int_C sin(x) dx + cos(y) dy=f(-3,2)-f(2,0)= -cos(-3) +sin 2 + cos 2`