Answer:
Step-by-step explanation:
mass of each drop, m = 1.8 mg = 1.8 x 10^-6 kg
Charge on each drop, q = 21 pC = 21 x 10^-12 C
distance, d = 0.44 cm = 0.0044 m
(a) The formula for the electrostatic force between them is given by
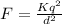
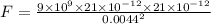
F = 2.05 x 10^-7 N
Thus, the force is 2.05 x 10^-7 N .
(b) Let a be the acceleration.
a = F / m
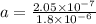
a = 0.114 m/s^2