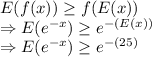Answer:
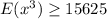
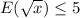
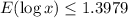
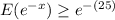
Explanation:
We are given the following information in the question:
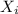 s a nonnegative random variable with mean 25
s a nonnegative random variable with mean 25
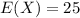
We have to find the following:
a) Since
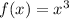 is a convex function,
is a convex function,
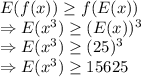
b) Since
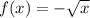 is a convex function,
is a convex function,
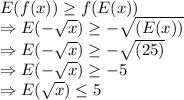
c) Since
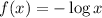 is a convex function,
is a convex function,
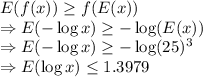
d) Since
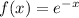 is a convex function,
is a convex function,