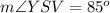Question

In the figure, mZRPZ = 95 and TU ||RQ|| VW. Find the measure of angle YSV.

Answer 1

`m\angle YSV=85^o`

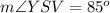
Explanation:

The complete question in the attached figure

step 1

Find the measure of angle QPZ

we kno that

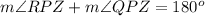`m\angle RPZ+m\angle QPZ=180^o` ---> by supplementary angles (form a linear pair)

we have

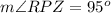`m\angle RPZ=95^o` ---> given value

substitute

`95^o+m\angle QPZ=180^o`

`m\angle QPZ=180^o-95^o`

`m\angle QPZ=85^o`

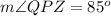
step 2

Find the measure of angle YSV

we know that

When two lines are crossed by another line, Alternate Exterior Angles are a pair of angles on the outer side of each of those two lines but on opposite sides of the transversal. If the two lines are parallel then the alternate exterior angles are congruent.

In this problem

The transversal is the line XY

The two parallel lines are RQ and VW

therefore

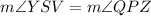`m\angle YSV=m\angle QPZ` ---> by alternate exterior angle

we have

`m\angle QPZ=85^o`

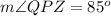
therefore

`m\angle YSV=85^o`