Question

a sealed cylinder contains a sample of ideal gas at a pressure of 2.0 atm. The rms speed of the molecules is v0. If the rms speed is then reduced to 0.90 v0, what is the pressure of the gas?

Answer 1

P_2 = 1.62 atm

Step-by-step explanation:

We know the formula for the rms speed of the ideal gas is given by

`v_(rsm)=\sqrt{(3PV)/(m) }`

P= pressure of the surrounding

V= volume of the vessel

m= mass of the gas

Now, From this formula rms speed (v_rms) is directly proportional to square root is pressure.

Then

`(v_(rsm,1))/(v_(rsm,2)) =\sqrt{(P_1)/(P_2) }`

given that v_rsm,1= v0

and v_rsm,2=0.9v0

putting these values we get

`(v0)/(0.9v0) =\sqrt{(2)/(P_2) }`

P_2 = 1.62 atm

Answer 2

The pressure of the gas is 1.8 atm.

Step-by-step explanation:

Given that,

Pressure of ideal gas= 2.0 atm

rms speed of the molecule = v₀

Reduced rms speed = 0.90 v₀

We know the formula of rms speed of the ideal gas

`v_(rms)=\sqrt{(3Pv)/(m)}`

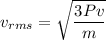
From this formula rms speed is directly proportional to square root is pressure.

We need to calculate the pressure of the gas

Using formula of rms speed

`(v_(rms))/(v_(rms))=\sqrt{(P_(1))/(P_(2))}`

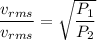
Put the value into the formula

`(v_(0))/(0.90v_(0))=\sqrt{(2.0)/(P_(2))}`

`P_(2)=2.0*0.90`

`P_(2)=1.8\ atm`

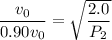
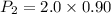
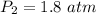
Hence, The pressure of the gas is 1.8 atm.