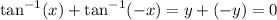Answer:
c)
Explanation:
To solve this, remember some properties of trigonometric functions.
Let
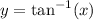 . Then, by definition of inverse function,
. Then, by definition of inverse function,
 . Multiply by -1 to both sides of this equation to get
. Multiply by -1 to both sides of this equation to get
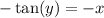 .
.
Note that
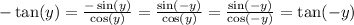 because sine is an odd function and cosine is an even function. Then
because sine is an odd function and cosine is an even function. Then
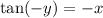 . Take the inverse tangent in both sides to get
. Take the inverse tangent in both sides to get
 .
.
Using the previous equations, we obtain: