Question

Emmy kicks a soccer ball up at an angle of 45° over a level field. She watches the ball\'s trajectory and notices that it lands, two seconds after being kicked, about 20 m away to the north. Assume that air resistance is negligable, and plot the horizontal and vertical components of the ball\'s velocity as a function of time. Consider only the time that the ball is in the air, after being kicked but before landing. Take \"north\" and \"up\" as the positive x and y directions, respectively, and use g ≈10 m/s2 for the downward acceleration due to gravity.

The answer is suppose to be in two graphs, One for horizontal velocity and the other for vertical velocity. Time along x-axis in .5sec increments.

Answer 1

vₓ = 10 m / s,
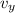`v_(y)` = 10 - 10 t

Step-by-step explanation:

This is a projectile launching exercise, where the x and y axes are treated independently.

On the x axis. towards the north there is no acceleration, so the speed is constant

vₓ = v₀ₓ

On the vertical y-axis, there is the acceleration of gravity with value (-g) is directed down, the equation is

`v_(y)` =
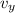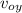`v_(oy)` - gt

Let's use trigonometry to find the initial velocity component

sin 45 =
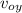`v_(oy)` / v₀

cos 45 = v₀ₓ / v₀

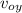`v_(oy)` = v₀ sin45

v₀ₓ = v₀ cos45

To find the initial velocity let's use the scope equation

R = v₀² sin 2θ / g

v₀ = √ Rg / sin 2θ

v₀ = √ (20 10 / sin (2 45))

v₀ = 14.14 m / s

With this value we find the initial velocity component

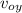`v_(oy)` = 14.14 sin 45

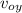`v_(oy)` = 10 m / s

v₀ₓ = 14.14 cos 45

v₀ₓ = 10 m / s

We get the equations to graph

X axis

vₓ = 10 m / s

In this graph it is a horizontal line

Y Axis

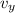`v_(y)` = 10 - 10 t

For this graph let's build a table

t (s)
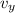`v_(y)` (m / s)

0 10

0.5 5

1.0 0

1.5 -5

2 -10

see attached for both curves