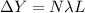Condition for diffraction
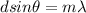
Where
a = Distance between slits
m = Order of the fringes
 = Wavelength
= Wavelength
 = At the angle between the ray of light and the projected distance perpendicular between the two objects
= At the angle between the ray of light and the projected distance perpendicular between the two objects
For small angles
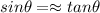
Where
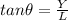
Where L is the distance between the slits and Y the length of the light.
Replacing we have
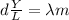
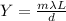
The distance between slits d can be expressed also as
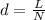 Where N is the number of the fringes, then
Where N is the number of the fringes, then
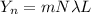
Similarly when there is added a new Fringe we have the change of the distance would be :
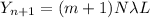
Linear distance between fringes is
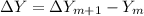
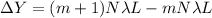
Therefore the answer is