Question

(a) Show that the vector field F = sin y cos x i + cos y sin x j + z k is conservative, or equivalently satisfies the equations of the (curl) component test. (b) Find a scalar potential function f(x, y, z) for the vector field F(x, y, z), and show all steps of your construction of f. (c) Evaluate the line integral ∫cF *dr where C is a path from the point A(0, 1, 0) to B(π/2, π/2, 2).

Answer 1

a. If a vector field
`\vec F` is conservative, then its curl is 0:

(Note that, generally, if the curl is 0, the field need not be conservative!)

b. If there is a scalar function
`f` for which
`\\abla f=\vec F`, then

`(\partial f)/(\partial x)=\sin y\cos x`

`(\partial f)/(\partial y)=\cos y\sin x`

`(\partial f)/(\partial z)=z`

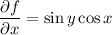
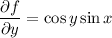
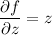
From these equations we find (first by integrating both sides of the first equation with respect to
`x`)

`f(x,y,z)=\sin y\sin x+g(y,z)`

`\implies(\partial f)/(\partial y)=\cos y\sin x=\cos y\sin x+(\partial g)/(\partial y)\implies(\partial g)/(\partial y)=0\implies g(y,z)=h(z)`

`\implies(\partial f)/(\partial z)=z=(\mathrm dh)/(\mathrm dz)\implies h(z)=\frac{z^2}2+C`

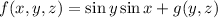
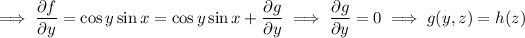
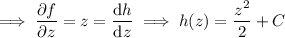
So we have

`\boxed{f(x,y,z)=\sin y\sin x+\frac{z^2}2+C}`

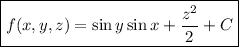
c. By the gradient theorem (i.e. fundamental theorem of calculus), we have for any path
`C` beginning at
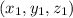`(x_1,y_1,z_1)` and terminating at
`(x_2,y_2,z_2)`

`\displaystyle\int_C\\abla f\cdot\mathrm d\vec r=f(x_2,y_2,z_2)-f(x_1,y_1,z_1)`

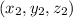
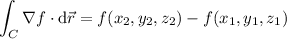
so that

`\displaystyle\int_C\vec F\cdot\mathrm d\vec r=f\left(\frac\pi2,\frac\pi2,2\right)-f(0,1,0)=\boxed3`