Answer:
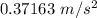
0.07576
0.13235
Step-by-step explanation:
 = Angular speed =
= Angular speed =

r = Distance from the center = 6.1 cm
g = Acceleration due to gravity = 9.81 m/s²
Acceleration of the seed would be
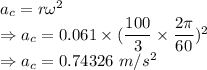
The acceleration of the seed is
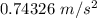
Frictional force is given by
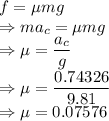
The coefficient of friction is 0.07576
Transverse acceleration is given by
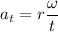
The resultant acceleration is given by
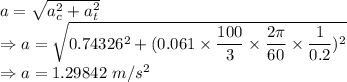
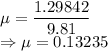
The coefficient of friction is 0.13235