Question

A leaky 12-kg bucket is lifted from the ground to a height of 15 m at a constant speed with a rope that weights 0.75 kg/m. Initially the bucket contains 40 kg of water, but the water leaks at a constant rate and finishes draining just as the bucket reaches the 15 m level. How much work is done

Answer 1

Approximately 5.5 kJ.

Step-by-step explanation:

• The mass of water in the bucket is
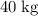  `\rm 40\; kg` at a height of 0 meters above the ground.
• At a height of 15 meters, the mass of the water would be
  `\rm 0\; kg`.

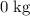The bucket goes up at a constant rate. Also, the water leaks at a constant rate. As a result, the mass of water in the bucket changes at a constant rate as height increases.

Find the rate at which the mass of water decreases over height:

`\begin{aligned} &\text{Rate at which water leaks}\cr  &= \frac{\text{Change in mass of Water}}{\text{Change in height}} \cr &= \rm (40 \; kg - 0\; kg)/(15\; m) \cr &= \rm (40)/(15)\; kg \cdot m^(-1)\end{aligned}`.

In other words,
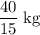`\displaystyle \rm (40)/(15)\; kg` of water leaks out of the bucket everytime its height increases by
`\rm 1\; m`.

Hence, the mass of water at
`h\; \rm m` would be
`\displaystyle 40 - (40)/(15)\, h`
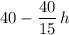
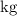`\rm kg`. Write that as a function of height:

`\displaystyle m_\text{water}(h) = 40 - (40)/(15)\, h = (40)/(15) \, (15 - h)`.

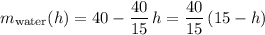On the other hand,
`(40 - h)\; \rm m` of rope is still in the air while the bucket is at a height of
`h\; \rm m`. The mass of the rope that needs to be lifted at would thus be
`0.75\; (15 - h)\; \rm kg`.

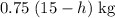Write that also as a function of the height of the bucket:

`\displaystyle m_\text{rope}(h) = 0.75\; (15 - h)`.

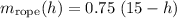Add the mass of the bucket:

`\displaystyle m(h) = (40)/(15)\, (15 - h) + 0.75\; (15 - h) + 12`.

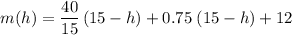Simplify this expression:

`\begin{aligned} m(h) &= (40)/(15)\, (15 - h) + 0.75\; (40 - h) + 12 \cr &= \left((40)/(15) + 0.75\right) (15 - h) + 12\end{aligned}`.

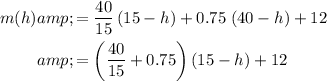The only two forces on the bucket are gravitational force and tension force from the rope. Since the bucket is moving at constant speed, the net force on it should be zero. The two forces must balance each other. In other words, they must act in opposite directions. Most importantly, the must be of equal magnitude. That is:

`\begin{aligned} F(h) &= W(h) \cr &= m(h) \cdot g \cr &= 9.81 * \left(\left((40)/(15) + 0.75\right) (15 - h) + 12\right)\cr &= 9.81 * \left((40)/(15) + 0.75\right) (15 - h) + 9.81 * 12 \cr &\approx 502.763 - 33.5175\; h + 117.72 \cr &= 620.483 - 33.5175\; h\end{aligned}`.

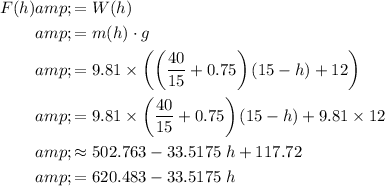Integrate force over distance travelled to find work done. In this case, since the bucket is moving upwards, distance travelled is equal to height.

`\begin{aligned}W &= \int \limits_(0)^(15) (620.483 - 33.5175\; h) \, dh \cr &= \left[620.483\; h - (1)/(2)* 33.5175\; h^2\right]^(15)_(0) \cr &= \left(620.483 * 15 - (1)/(2) * 33.5175 * 15^2\right) - 0 \cr &\approx 5.5* 10^(3)\; \rm J \cr &= 5.5\;\rm kJ \end{aligned}`.