Answer:
See Explanation below
Explanation:
Topic: Gradient and Slope
To get the other points, first, we must calculate the equation of the line using the slope formula.
Given
Point (0, -1)
Slope, m = 2
The Slope of a line is calculated by
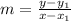
Given that a point on the line is (0, -1), then
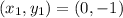
Substitute each of these values in the formula above, we have
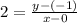
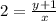
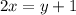 --- Make y the subject of formula
--- Make y the subject of formula
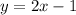
This equation can then be used to get the other points that lies on the slope.
Take for instance Point
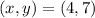
By Substitution, we have
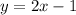 becomes
becomes

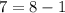
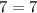
Hence, the point
 lies on the plane
lies on the plane