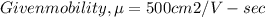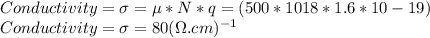Answer:
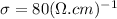
Step-by-step explanation:
Na = Acceptor Concentration (cm-3) = 0
Nd = Donor Concentration (cm-3) =
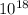
 = Resistivity (Unit: ohm-cm)
= Resistivity (Unit: ohm-cm)
n = electron concentration (cm-3)
q =Charge on electron =
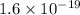
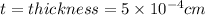
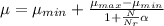

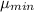
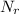 are fit parameter
are fit parameter
Arsenic is used
 =52.2
=52.2
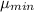 =1417
=1417
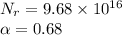
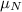 =222.2
=222.2
For n type =
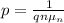
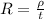
(ND>>NA ---> n-type) // Here The p-type sample is converted to n-type material by adding more donors than acceptors
n=ND-NA =1018/cm3
![\rho=[1.6*10-19*1018*222.2]-1 = 0.28 (ohm-cm)](https://img.qammunity.org/2020/formulas/physics/college/kr90h2zrig26i8cghdg6botugiwdtwd1yx.png)
R=0.28/5*10-4=560