Question

1.(16 pts.) Find the volume of the solid obtained by revolving the region enclosed by y = xex , y = 0 and x = 1 about the x-axis.

Answer 1

The Volume is 5.018 cubic units

Step-by-step explanation:

Volume Of A Solid Of Revolution

Let f(x) be a continuous function defined in an interval [a,b], if we take the area enclosed by f(x) between x=a, x=b and revolve it around the x-axis, we get a solid whose volume can be computed as

`\displaystyle V=\pi \int_a^bf^2(x)dx`

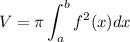
It's called the disk method. There are other available methods to compute the volume.

We have

`f(x)=xe^x`

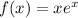
And the boundaries defined as x=1, y=0 and revolved around the x-axis. The left endpoint of the integral is easily identified as x=0, because it defines the beginning of the region to revolve. So we need to compute

`\displaystyle V=\pi \int_0^1(xe^x)^2dx=\pi \int_0^1x^2e^(2x)dx`

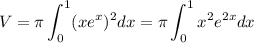
We need to first determine the antiderivative

`\displaystyle I=\int x^2e^(2x)dx`

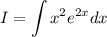
Let's integrate by parts using the formula

`\displaystyle \int u.dv=u.v-\int v.du`

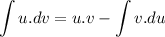
We pick
`u=x^2,\ dv=e^(2x)dx`

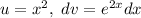
Then
`du=2xdx,\ v=(e^(2x))/(2)`

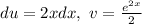
Applying by parts:

`\displaystyle I=x^2(e^(2x))/(2)-\int 2x(e^(2x))/(2)dx`

`\displaystyle I=(x^2e^(2x))/(2)-\int xe^(2x)dx`

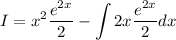
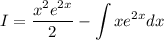
Now we solve

`\displaystyle I_1=\int xe^(2x)dx`

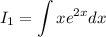
Making
`u=x,\ dv=e^(2x)dx`

`\displaystyle du=dx,\ v=(e^(2x))/(2)`

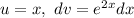
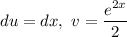
Applying by parts again:

`\displaystyle I_1=x(e^(2x))/(2)-\int (e^(2x))/(2)dx`

`\displaystyle I_1=(xe^(2x))/(2)-(1)/(2)\int e^(2x)dx`

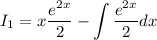
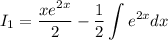
The last integral is directly computed

`\displaystyle \int e^(2x)dx=(e^(2x))/(2)`

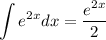
Replacing every integral computed above

`\displaystyle I=(x^2e^(2x))/(2)-\left((xe^(2x))/(2)-(1)/(2)(e^(2x))/(2)\right)`

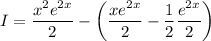
Simplifying

`\displaystyle I=\frac{\left(2x^2-2x+1\right)\mathrm{e}^(2x)}{4}`

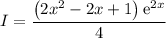
Now we compute the definite integral as the volume

`V=\pi \left[\frac{\left(2(1)^2-2(1)+1\right)\mathrm{e}^(2(1))-\left(2(0)^2-2(0)+1\right)\mathrm{e}^(2(0))}{4}\right]`

Finally

`V=\pi \frac{\mathrm{e}^2-1}{4}=5.018`

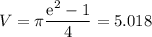
The Volume is 5.018 cubic units