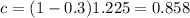Answer:
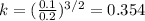
In the steady state level of Country A, the capital per worker is 0.354
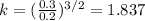
In th steady state level of country B, the capital per worker is 1.387.
Now we can find the steady level income per worker like this:
Country A
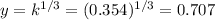
Country B:
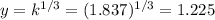
And if we want to find the consumption per worker we can apply this formula:
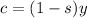
Country A
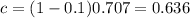
Country B
Step-by-step explanation:
We assume that we have a common production function for country A and B given by:

And we can find the per worker production function
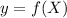 like this:
like this:
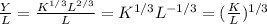
And we can express the function just in terms of a constant like this:
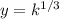
From the info given by the problem we have:
Depressciation
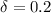
Savings for A
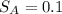
Savings for B
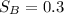
And we assume that
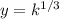
Let's begin finding the steady state level of capital per worker, we need to satisfy the following condition:
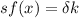
The reason is because. The growth of capital per worker
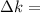 is given by investment per worker
is given by investment per worker
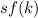 minus the depreciation per worker
minus the depreciation per worker
 , and we have then
, and we have then
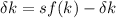 and if is steady then k=0.
and if is steady then k=0.

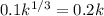
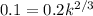
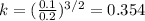
In the steady state level of Country A, the capital per worker is 0.354. For country B we can do a similar procedure like this:
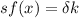
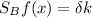
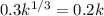

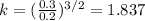
In the steady state level of country B, the capital per worker is 1.387.
Now we can find the steady level income per worker like this:
Country A
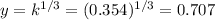
Country B:
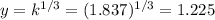
And if we want to find the consumption per worker we can apply this formula:
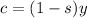
Country A
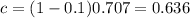
Country B