Question

you and a friend of your choice are driving to the island of chincoteague in virginia in two different cars. you are traveling 65 miles per hour and your friend is traveling 51 miles per hour. your friend has a 35-mile head start. the island of cincoteague is about 200 miles from philadelhia. when will you catch up with your friend

Answer 1

They will catch up at 2.5 hours

Explanation:

Constant Speed Motion

It refers to situations where objects move at the same speed in the same direction. The speed is computed as the ratio of the distance x to the time

`\displaystyle v=(x)/(t)`

The situation pictured in the question requires the computation of distances traveled by two objects running at different speeds. The slower car goes ahead with a 35-mile head start, so it's just a matter of time when the fastest car and the slower will catch up. We'll use here the concept of relative speed to easily solve the problem.

The speed of the first friend is

`v_1=51\ mph`

And the speed of the second friend is

`v_2=65\ mph`

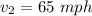
If the first friend was at rest, the second friend will have a relative speed of

`v_r=65-51=14\ mph`

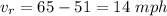
The distance between them (35 miles) will be covered in a time t which can be found from

`\displaystyle v_r=(x)/(t)`

`\displaystyle t=(x)/(v_r)`

`\displaystyle t=(35)/(14)=2.5\ hours`

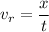
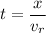
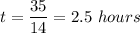
We need to check if they have not arrived to chincoteague by that time. We'll compute the distance of the fastest friend

`x_2=65*2.5=162.5\ miles`

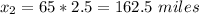
We can see they catch up (200-162.5=37.6 miles) before arriving to their destiny.

Just to verify, the distance traveled by the first friend is

`x_2=51*2.5=127.5\ miles`

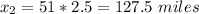
The difference of those distances is 162.5-127.5=35 miles, exactly the original head-start