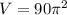Answer:
a)

b)
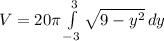
c)
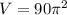
Step-by-step explanation
In order to solve these problems, we must start by sketching a drawing of what the graph of the problem looks like, this will help us analyze the drawing better and take have a better understanding of the problem (see attached pictures).
a)
On part A we must build an integral for the volume of the torus by using the shell method. The shell method formula looks like this:
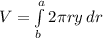
Where r is the radius of the shell, y is the height of the shell and dr is the width of the wall of the shell.
So in this case, r=x so dr=dx.
y is given by the equation of the circle of radius 3 centered at (5,0) which is:
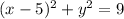
when solving for y we get that:
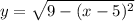
we can now plug all these values into the shell method formula, so we get:
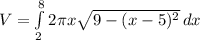
now there is a twist to this problem since that will be the formula for half a torus.Luckily for us the circle is symmetric about the x-axis, so we can just multiply this integral by 2 to get the whole volume of the torus, so the whole integral is:
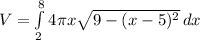
we can take the constants out of the integral sign so we get the final answer to be:

b)
Now we need to build an integral equation of the torus by using the washer method. In this case the formula for the washer method looks like this:
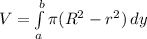
where R is the outer radius of the washer and r is the inner radius of the washer and dy is the width of the washer.
In this case both R and r are given by the x-equation of the circle. We start with the equation of the circle:
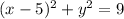
when solving for x we get that:

the same thing happens here, the square root can either give you a positive or a negative value, so that will determine the difference between R and r, so we get that:

and
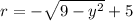
we can now plug these into the volume formula:
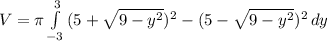
This can be simplified by expanding the perfect squares and when eliminating like terms we end up with:
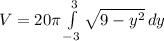
c) We are going to solve the integral we got by using the washer method for it to be easier for us to solve, so let's take the integral:
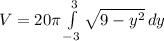
This integral can be solved by using trigonometric substitution so first we set:
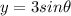
which means that:
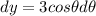
from this, we also know that:

so we can set the new limits of integration to be:
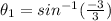
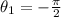
and

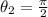
so we can rewrite our integral:

which simplifies to:
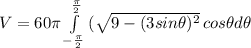
we can further simplify this integral like this:
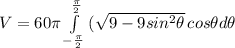
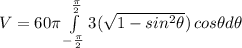
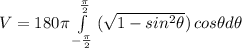
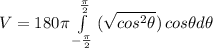
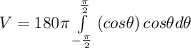
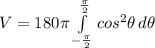
We can use trigonometric identities to simplify this so we get:
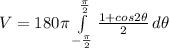
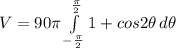
we can solve this by using u-substitution so we get:
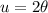
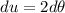
and:
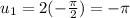
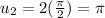
so when substituting we get that:
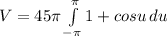
when integrating we get that:
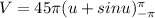
when evaluating we get that:
![V=45\pi[(\pi+0)-(-\pi+0)]](https://img.qammunity.org/2020/formulas/physics/college/a7mxep4nh25r33ow8mnhapqwtujtf2qnmb.png)
which yields: