Question

Let A = {2, 3, 4, 5} Let B = {3, 4, 5, 6} Let S be the divides relation, so for all (x,y) (x|y means x divides into y) a. State explicitly which ordered pairs are in S and S-1.

Answer 1

S={(2,4),(2,6),(3,3),(3,6),(4,4),(5,5)}

S^-1={(4,2),(6,2),(3,3),(6,3),(4,4),(5,5)}

Explanation:

The relation S⊆A×B is defined as the set
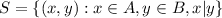`S=\(x,y): x\in A, y\in B, x`. If x=2, we have that 2|4 and 2|6 and 4,6 are the anly elements of B that 2 divides, then the ordered pairs (2,4),(2,6) are elements of S. If x=3, 3|3 and 3|6 so (3,3),(3,6)∈S (these are all the possibilities for x=3). Similarly, 4|4 and 5|5 then (4,4),(5,5)∈S.

The inverse relation is defined as
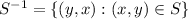`S^(-1)=\{(y,x): (x,y)\in S\}` so we obtain the pairs from S^-1 reversing the order from those in S. We can also interpret S^-1 as
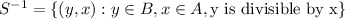`S^(-1)=\{(y,x): y\in B, x\in A,\text{y is divisible by x}\}`.