Question

Let x be per capita income in thousands of dollars. Let y be the number of medical doctors per 10,000 residents. Six small cities in Oregon gave the following information about x and y.

Answer 1

The percentage of variation esplained by the model is given by the determination coefficient, on this case:

`R^2 = 0.934^2 =0.872`

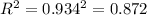
And we have 87.2% of the variation explained by the linear model given.

`\hat y = 5.756(8.5) -36.895=12.031`

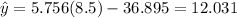
And we have 12.031 doctors per 10000 residents.

Step-by-step explanation:

Assuming the following dataset:

x y

8.6 9.6

9.3 18.5

10.1 20.9

8.0 10.2

8.3 11.4

8.7 13.1

Assuming this question: "The data has a correlation coefficient of r = 0.934. Calculate the regression line for this data. What percentage ofvariation is explained by the regression line? Predict the number of doctors per 10,000 residents in a town with a per capita income of $8500."

We want a linear model like this:

`y = mx +b`

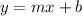
Where m represent the slope and b the intercept for the linear model. And we cna find the slope and b with the following formulas:

`m = (n \sum xy - \sum x \sum y)/(n \sum x^2 -(\sum x)^2)`

`b = (\sum y)/(n) -m (\sum x)/(n)`

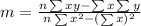
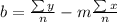
And from the dataset we have the following values:

`n= 6, \sum x =53, \sum y = 83.7 , \sum xy = 755.89, \sum x^2 = 471.04`

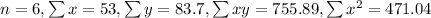
And replacing into the equation for m we got:

`m =(6(755.89) - (53)(83.7))/(6(471.04) -(53)^2)=5.756`

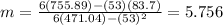
And the intercept:

`b = (83.7)/(6)-36.895 5.756 (53)/(6)=-36.895`

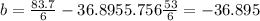
And then the linear model is given by:

`\hat y = 5.756 x -36.895`

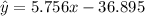
We can find the estimation replacing x = 8.5 into the linear model and we got:

`\hat y = 5.756(8.5) -36.895=12.031`

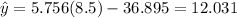
And we have 12.031 doctors per 10000 residents.

The percentage of variation esplained by the model is given by the determination coefficient, on this case:

`R^2 = 0.934^2 =0.872`

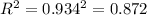
And we have 87.2% of the variation explained by the linear model given.