Question

Need help on these 2 questions and my last 2 uploads !! Help! please

Answer 1

19.
`(3\pi)/(2)`

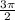
20. The work is the answer

Explanation:

19. We begin with the equation (for my ease, I will swap theta with x)

`sin(x)+1=cos^(2) (x)`

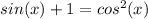
First, we can use the Pythagorean Identity to substitute in
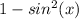`1-sin^(2) (x)` for
`cos^(2) (x)`

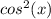
This gives us

`sin(x)+1=1-sin^(2) (x)`

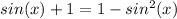
Next, we can subtract 1 from each side

`sin(x)=-sin^(2) (x)`

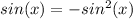
Now, we can divide each side by
`sin(x)`

`1=-sin(x)`

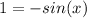
Now we move the negative to the other side

`sin(x)=-1`

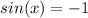
Now we can do the inverse of sin to find our value

`x=sin^(-1) (-1)`

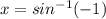
With this inverse, we are looking for an angle that has the sin (or the y value) of -1. As this is an inverse sin function, it has the domain restriction of

`[-(\pi )/(2) ,(\pi )/(2)]`.

From this information, we find that
`x=-(\pi)/(2)`

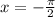
But this answer does not fit the initial interval that we were given. Luckily,
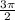`(3\pi)/(2)` is the same location as
`(\pi)/(2)`, so that is our answer.

20. We begin with the expression
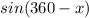`sin(360-x)` and we have to prove that it is equal to
`-sin(x)`

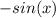
First, we need to use the Difference of 2 Angles Trig Identity. This says:

`sin(\alpha -\beta )=sin(\alpha) cos(\beta) -cos(\alpha) sin(\beta)`

When we apply this to our expression, we get

`sin(360) cos(x) -cos(360) sin(x)`

Next, we can simplify our the two finite aspects

`sin(360)=0\\\\cos(360)=1`

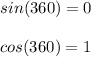
When we plug in these two values, we get

`(0) cos(x) -(1) sin(x)`

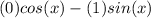
This simplifies to
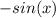`-sin(x)` which is what we were trying to verify.