Question

A tensile test was made on a tensile specimen, with a cylindrical gage section which had a diameter of 10 mm, and a length of 40 mm. After fracture, the length of the gage section was found to be 50 mm, the reduction in area 90 percent, and the load at fracture 1000 N. Compute: a) b) c) d) The specimen elongation. The engineering fracture stress. The true fracture stress. The true strain at the neck. Note: the reduction in area is defined as the initial area, minus the final area, divided by the initial area

Answer 1

The answers are as follow:

a) 10 mm

b) 12.730 N/
`mm^(2)`

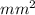
c) 127.307 N/
`mm^(2)`

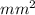
d) 0.25

Step-by-step explanation:

d1 = 10mm , L1 = 40 mm, L2 = 50 mm, reduction in area = 90% = 0.9

Force = F =1000 N

let us find initial area first, A1 = pi*
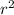`r^(2)` = 78.55
`mm^(2)`

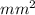
using reduction in area formula : 0.9 = (A1 - A2 ) / A1

solving it will give, A2 = 0.1 A1 = 7.855
`mm^(2)`

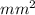
a) The specimen elongation is final length - initial length

50 - 40 = 10 mm

b) Engineering stress uses the original area for all stress calculations,

Engineering stress = force / original area = F / A1 = 1000 / 78.55

Engineering stress = 12.730
`N / mm^(2)`

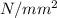
c) True stress uses instantaneous area during stress calculations,

True fracture stress = force / final area = F / A2 = 1000 / 7.855

True Fracture stress = 127.30
`N / mm^(2)`

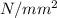
e) strain = change in length / original length

strain = 10 / 40 = 0.25