Question

Megan Brink is offered the possibility of investing $6,651 today at 6% interest per year in a desire to accumulate $10,000.

Answer 1

7 years.

Step-by-step explanation:

We know,

Future value = Present Value ×
`(1 + i)^(n)`

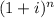
Given,

Future Value, FV = $10,000

Present Value, PV = $6,651

Interest rate, i = 6% = 0.06

We have to determine how many years to acquire $10,000 in the future.

Now, $10,000 = $6,651 ×
`(1 + 0.06)^(n)`

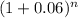
or, $(10,000 ÷ 6,651) =
`1.06^(n)`

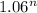
or, 1.5035 =
`1.06^(n)`

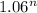
or, Log 1.5035 = n log 1.06

Using the calculator to find the value of log.

0.1771 = n × 0.0253

or, n = 0.1771 ÷ 0.0253

or, n = 7 years

7 years will be needed to acquire $10,000 in the future.