Answer:
The train can be made up in a total of
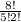 ways
ways
Explanation:
FIrst, lets assume that all cars are distinct. If that is the case, then, since we have a total of 8 cars, we have
- 8 possibilities for the first car
- 7 possibilities for the second car
- 6 possibilities for the third car
and so on.
So we have a total of 8! = 8*7*6*...*3*2*1 possibilities to make a train.
Now lets take into account that 5 of the cars are identical within each other. Then we could make a permutation of those 5 cars and we wouldnt notice. Hence, the order of the 5 cars of second-class doesnt matter and as a result, we should divide 8! by the total of possible permutations of the 5 second class cars, that it, 5!
We also need to divide the result by 2! = 2, because which first class car came first doesnt matter either. Therefore, the train can be made up in a total of
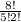 ways.
ways.