Answer:
![r=(9(5316)-(70)(740))/(√([9(704) -(70)^2][9(62078) -(740)^2]))=-0.9908](https://img.qammunity.org/2020/formulas/mathematics/college/8dfs3pzk4mmq0dcou0jjlr06ozeh9i6368.png)
Explanation:
Previous concepts
The correlation coefficient is a "statistical measure that calculates the strength of the relationship between the relative movements of two variables". It's denoted by r and its always between -1 and 1.
Solution to the problem
In order to calculate the correlation coefficient we can begin doing the following table:
n x y xy x*x y*y
1 2 100 200 4 10000
2 5 88 440 25 7744
3 8 82 656 64 6724
4 6 84 504 36 7056
5 11 73 803 121 5329
6 4 94 376 16 8836
7 17 57 969 289 3249
8 10 78 780 100 6084
9 7 84 588 49 7056
And in order to calculate the correlation coefficient we can use this formula:
![r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))](https://img.qammunity.org/2020/formulas/mathematics/middle-school/h2kbdui9ydpsixheffu6h8g6vjzzbhe9ox.png)
For our case we have this:
n=9
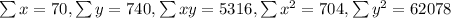
![r=(9(5316)-(70)(740))/(√([9(704) -(70)^2][9(62078) -(740)^2]))=-0.9908](https://img.qammunity.org/2020/formulas/mathematics/college/8dfs3pzk4mmq0dcou0jjlr06ozeh9i6368.png)