Question

The path of a launched missile can be modeled by a quadratic function. Explain how you would use the function to determine the greatest height the rocket reaches and the horizontal distance it travels before reaching the ground. Answer in complete sentences.

Answer 1

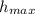`h_(max)`=u^2/2a

s=ut

Step-by-step explanation:

The path of a launched missile can be modeled by a quadratic function. Explain how you would use the function to determine the greatest height the rocket reaches and the horizontal distance it travels before reaching the ground. Answer in complete sentences.

from the newton's equation of motion , we can use the equation

s=ut+1/2at^2

s=h

a=g

g=acceleration due to gravity

t=time

u=initial velocity

h=height of the launched missile

the vertical component of the flight of the missile should be

h=1/2at^2, notice that it is going travelling against gravity

also V^2=u^2+2ah

at maximum height , final velocity becomes zero

-u^2=-2ah

u=
`√(2ah)`

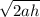
or
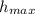`h_(max)`=u^2/2a

take not that the initial velocity has both a vertical component and horizontal component,

s=ut+1/2at^2

to get the horizontal distanced moved , we write

s=ut.....................

time is independent on the horizontal and vertical component

Answer 2

The highest point is at witch the rocket stops to going up and starts to going down, this point will is the vertex of the quadratic equation, this point is the zero of the first derivate of the quadratic equation, so if the quadratic equation is:

y = a*x^2 + b*x + c

the first derivate will be:

v = 2a*t + b

now we find the x in which v = 0

x = -b/2a

Now, we replace this time in the first equation and find the max height.

Y = a*(-b/2a)^2 + b*-b/2a + c

if it is trhowed from the ground, then c = 0, the horizontal distance will be when Y is zero again:

Y = a*x^2 + b*x

is zero at x = 0, we must find the other root.

Y = (a*x + b)*x

so x = -b/a

Then the horizontal distance traveled is x = -b/a, that is the horizontal distance at which the rocket hits the ground again.