Question

When of benzamide are dissolved in of a certain mystery liquid , the freezing point of the solution is less than the freezing point of pure . Calculate the mass of ammonium chloride that must be dissolved in the same mass of to produce the same depression in freezing point. The van't Hoff factor for ammonium chloride in .

Answer 1

The given question is incomplete. The complete question is as follows.

When 70.4 g of benzamide (
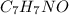`C_(7)H_(7)NO`) are dissolved in 850 g of a certain mystery liquid X, the freezing point of the solution is
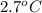`2.7^(o)C` lower than the freezing point of pure X. On the other hand, when 70.4 g of ammonium chloride (
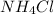`NH_(4)Cl`) are dissolved in the same mass of X, the freezing point of the solution is
`9.9^(o)C` lower than the freezing point of pure X.

Calculate the Van't Hoff factor for ammonium chloride in X.

Step-by-step explanation:

First, we will calculate the moles of benzamide as follows.

Moles of benzamide =
`\frac{mass}{\text{Molar mass of benzamide}}`

=
`(70.4 g)/(121.14 g/mol)`

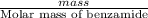
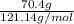
= 0.58 mol

Now, we will calculate the molality as follows.

Molality =
`\frac{\text{moles of solute (benzamide)}}{\text{solvent mass in kg}}`

=
`(0.58 mol)/(0.85 kg)`

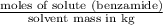
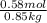
= 0.6837

It is known that relation between change in temperature, Van't Hoff factor and molality is as follows.

dT =
`i * K_(f) * m`,

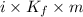where, dT = change in freezing point =
`2.7^(o)C`

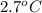
i = van't Hoff factor = 1 for non dissociable solutes

`K_(f)` = freezing point constant of solvent

m = 0.6837

Therefore, putting the given values into the above formula as follows.

dT =
`i * K_(f) * m`,

`2.7^(o)C = 1 * K_(f) * 0.6837 m`

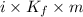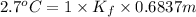
`K_(f)` = 3.949 C/m

Now, we use this
`K_(f)` value for calculating i for
`NH_(4)Cl`

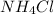
So, moles of ammonium chloride are calculated as follows.

Moles of
`NH_(4)Cl = (70.4 g)/(53.491 g/mol)`

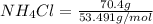
= 1.316 mol

Hence, calculate the molality as follows.

Molality =
`(1.316 mol)/(0.85 kg)`

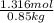
= 1.5484

It is given that value of change in temperature (dT) =
`9.9^(o)C`. Thus, calculate the value of Van't Hoff factor as follows.

dT =
`i * K_(f) * m`

`9.9^(o)C = i * 3.949 C/m * 1.5484 m`

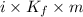
i = 1.62

Thus, we can conclude that the value of van't Hoff factor for ammonium chloride is 1.62.