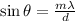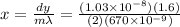Question

In a double-slit experiment, the third-order maximum for light of wavelength 500nm is located 11mm from the central bright spot on a screen 1.6m from the slits. Light of wavelength 670nm is then projected through the same slits.

How far from the central bright spot will the second-order maximum of this light be located?

Answer 1

The second-order maximum is located at 12 mm from the central bright.

Step-by-step explanation:

The equation that describes double-slit experiment is:

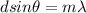`dsin\theta=m\lambda`(1)

with m:order of the maximum, d:distance between holes, λ:wavelength, θ: angular position of the maximum

We have to use the data given for the 500nm light to find the distance between the holes to use this value later with the 670nm light, so solving (1) for d:

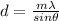`d=(m\lambda)/(sin\theta)`(2)

Because the distance between the screen and the slit (y) is a lot bigger than the distance between the first maximum from the central bright (x), we can use the approximation:

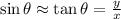`\sin\theta\approx\tan\theta=(y)/(x)`(3)

Using (3) on (2)

`d=(m\lambda x)/(y)=((3)(500*10^(-9))(11*10^(-3)))/(1.6)`

`d\approx1.03*10^(-8)\,m`

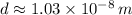
Now with the value of d we can use it to calculate how far from the central bright spot will the second-order maximum is for a 670nm light using (1) and (3) solving for x:

`\sin\theta=(m\lambda)/(d)`

`(y)/(x)=(m\lambda)/(d)`

`x=(dy)/(m\lambda)=((1.03*10^(-8))(1.6))/((2)(670*10^(-9)))`

`x\approx0.012\,m\approx12\text{\,}mm`