Answer:

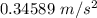
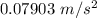
Step-by-step explanation:
M = Mass of Uranus
G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²
r = Radius of Uranus = 25360 km
h = Altitude = 104000 km
 = Radius of Miranda = 236 km
= Radius of Miranda = 236 km
m = Mass of Miranda =

Acceleration due to gravity is given by
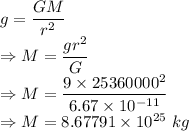
The mass of Uranus is

Acceleration is given by
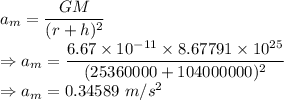
Miranda's acceleration due to its orbital motion about Uranus is
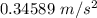
On Miranda
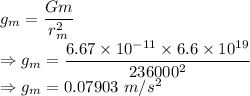
Acceleration due to Miranda's gravity at the surface of Miranda is
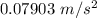
No, both the objects will fall towards Uranus. Also, they are not stationary.