Question

From the top of the hill , the angles of depression of two consecutive kilometer stones due east are found to be 30 and 45 degrees, find the height of the hill

Answer 1

The height of hill is 1.366 km

Solution:

The figure is attached below

Let AB is the height of the hill and two stones are C and D respectively where depression is 45 degree and 30 degree

The distance between C and D is 1 km

CD = 1 km

Here depression and hill has formed right angle triangles with the base

To find: height of hill

height of hill = AB

In triangle ABC,

`tan 45 = (height)/(base)`

`tan 45 = (AB)/(BC)`

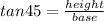
We know tan 45 (in degrees) = 1

`1 = (AB)/(BC)`

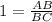
AB = BC ----- eqn 1

In triangle ABD,

`tan 30 = (AB)/(BD)`

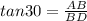
From attached figure, BD = BC + CD

Also we know that,

`tan 30 = (1)/(√(3)) = (1)/(1.732)`

`(1)/(1.732) = (AB)/(BC + CD)`

As AB = BC from eqn 1 and CD = 1 km,

`(1)/(1.732) = (AB)/(AB + 1)`

`1.732AB = AB + 1`

`1.732AB -AB = 1\\\\AB( 1.732 - 1) = 1\\\\AB(0.732) = 1\\\\AB = (1)/(0.732)\\\\AB = 1.366`

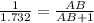
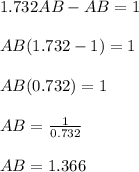
Hence the height of hill is 1.366 km