Question

Suppose the earth suddenly came to halt and ceased revolving around the sun. The gravitational force would then pull it directly to the sun. What would be the earth's speed as it crashed?

Answer 1

613373.65233 m/s

Step-by-step explanation:

M = Mass of Sun =
`1.989* 10^(30)\ kg`

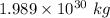
m = Mass of Earth

v = Velocity of Earth

r = Distance between Earth and Sun =
`147.12* 10^(9)\ m`

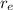`r_e` = Radius of Earth =
`6.371* 10^6\ m`

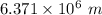
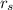`r_s` = Radius of Sun =
`695.51* 10^6\ m`

In this system it is assumed that the potential and kinetic energies are conserved

`(1)/(2)Mv_2-(GMm)/(r_e+r_s)=0-(GMm)/(r)\\\Rightarrow v=\sqrt{2GM((1)/(r_e+r_s)-(1)/(r))}\\\Rightarrow v=\sqrt{2* 6.67* 10^(-11)* 1.989* 10^(30)((1)/(6.371* 10^6+695.51* 10^6)-(1)/(147.12* 10^(9)))}\\\Rightarrow v=613373.65233\ m/s`

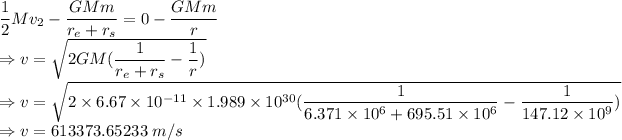
The velocity of Earth would be 613373.65233 m/s