Question

In a photoelectric-effect experiment it is observed that no current flows unless the wavelength is less than 570 nm .

A) What is the work function of this material?
B) What is the stopping voltage required if light of wavelength 420 nm is used?

Answer 1

(a) 3.49 x 10^-19 J

(b) 0.78 V

Step-by-step explanation:

threshold wavelength, λo = 570 nm = 570 x 10^-9 m

(A) the work function of the metal is given by

`\phi =(hc)/(\lambda _(0))`

where h is the Plank's constant and c be the speed of light.

h = 6.63 x 10^-34 Js

c = 3 x 10^8 m/s

`\phi =(6.63* 10^(-34)* 3 * 10^(8))/(570* 10^(-9))`

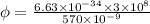
Ф = 3.49 x 10^-19 J

(B) λ = 420 nm = 420 x 10^-9 m

Use Einstein relation

`(hc)/(\lambda )=\phi +eV_(0)`

where, Vo is the stopping potential

`(6.63*10^(-19)* 3* 10^(8))/(420* 10^(-9) )=3.49 * 10^(-19) +eV_(0)`

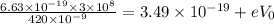
eVo = 1.246 x 10^-19

Vo = 0.78 V

Answer 2

`2.17960625\ eV`

0.77842 V

Step-by-step explanation:

h = Planck's constant =
`6.626* 10^(-34)\ m^2kg/s`

c = Speed of light =
`3* 10^8\ m/s`

`\lambda` = Wavelength

Work function is given by

`W=(hc)/(\lambda)\\\Rightarrow W=(6.626* 10^(-34)* 3* 10^8)/(570* 10^(-9))\\\Rightarrow W=3.48737* 10^(-19)\ J=(3.48737* 10^(-19))/(1.6* 10^(-19))=2.17960625\ eV`

The work function is
`2.17960625\ eV`

Stopping voltage is given by

`eV_0=hf-W_0\\\Rightarrow eV_0=(6.626* 10^(-34)* 3* 10^8)/(1.6* 10^(-19)* 420* 10^(-9))-2.17960625\\\Rightarrow eV_0=0.77842\ eV\\\Rightarrow V_0=0.77842\ V`

The stopping voltage required is 0.77842 V