Answer: 99% of confidence interval for the population proportion of employed individuals who work at home at-least once per week
//0.20113,0.20887[/tex]
Explanation:
step 1:-
Given sample size n=200
of the 200 employed individuals surveyed 41 responded that they did work at home at least once per week
Population proportion of employed individuals who work at home at least once per week P =
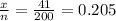
Q=1-P= 1-0.205 = 0.705
step 2:-
Now
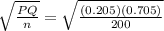
=0.0015
step 3:-
Confidence intervals
using formula
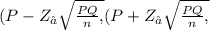
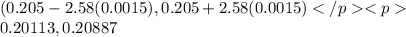
=0.20113,0.20887[/tex]
conclusion:-
99% of confidence interval for the population proportion of employed individuals who work at home at-least once per week
//0.20113,0.20887[/tex]