Answer:
a)
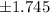
b)

c)

d)

Explanation:
We are given the following information in the question:
Confidence interval:
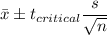
We have to find the appropriate t critical values for each of the following confidence levels and sample sizes:
a) 90% confidence, n = 17
Degree of freedom = n - 1 = 16

b) 90% confidence, n = 12
Degree of freedom = n - 1 = 11
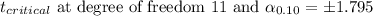
c) 99% confidence, n = 24
Degree of freedom = n - 1 = 23
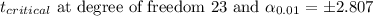
d) 99% confidence, n = 25
Degree of freedom = n - 1 = 24
