Answer:
 .
.
Explanation:
Use the binomial theorem: given any variables a,b and a positive integer n,
 .
.
In this case, take
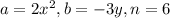
Usually, the terms on a polynomial of two variables are ordered starting with the highest power of x (x^12 in this case) and the lowest power of y. The powers of x decrease and the powers of y increase, so the last term has the highest power of y and the lowest power of x .
Then, the second term is k=1 as it has the second highest power of x, so replacing these values this term is:
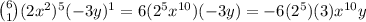 .
.