Answer:
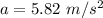
Step-by-step explanation:
It is given that,
Angle of inclination of the sled,
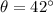
The coefficient of kinetic friction on ice is,
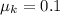
Using the free body diagram, the magnitude of the acceleration of a sled that is heading down is given by :
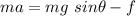
f is the frictional force
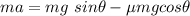
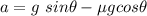
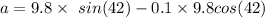
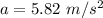
So, the magnitude of the acceleration of a sled is
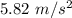 . hence, this is the required solution.
. hence, this is the required solution.