Answer:
1)
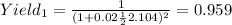
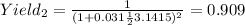
2)

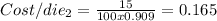
3)
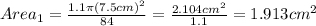
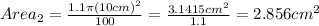
And for the new yield we need to take in count the increase of 15% for the area and we got this:
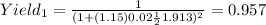
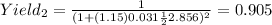
4)
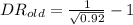 =0.0426 defects/cm^2
=0.0426 defects/cm^2
 =0.0260defects/cm^2
=0.0260defects/cm^2
Explanation:
Part 1
For this part first we need to find the die areas with the following formula:
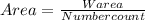
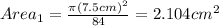
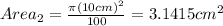
Now we can use the yield equation given by:
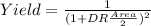
And replacing we got:
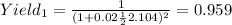
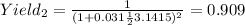
Part 2
For this part we can use the formula for cost per die like this:
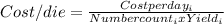
And replacing we got:

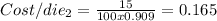
Part 3
For this case we just need to calculate the new area and the new yield with the same formulas for part a, adn we got:
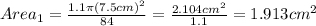
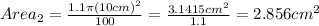
And for the new yield we need to take in count the increase of 15% for the area and we got this:
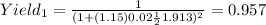
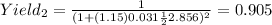
Part 4
First we can convert the area to cm^2 and we got 2 cm^2 the yield would be on this case given by:
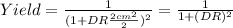
And if we solve for the Defect rate we got:

Now we can find the previous and new defect rate like this:
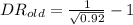 =0.0426 defects/cm^2
=0.0426 defects/cm^2
And for the new defect rate we got:
 =0.0260defects/cm^2
=0.0260defects/cm^2