Question

The number of messages arriving at a multiplexer is a Poisson random variable with mean 15 messages/second. Use the central limit theorem to estimate the probability that more than 950 message arrive in one minute.

Answer 1

0.048 is the probability that more than 950 message arrive in one minute.

Explanation:

We are given the following information in the question:

The number of messages arriving at a multiplexer is a Poisson random variable with mean 15 messages/second.

Let X be the number of messages arriving at a multiplexer.

Mean = 15

For poison distribution,

Mean = Variance = 15

`\text{Standard Deviation} = \sqrt{\text{Variance}} = √(15) = 3.872`

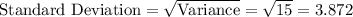
From central limit theorem, we have:

`z = \displaystyle(x-n\mu)/(\sigma√(n))`

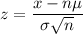
where n is the sample size.

Here, n = 1 minute = 60 seconds

P(x > 950)

`P( x > 950) = P( z > \displaystyle(950 - (60)(15))/(√((15)(60)))) = P(z > 1.667)`

`= 1 - P(z \leq 1.667)`

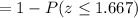
Calculation the value from standard normal z table, we have,

`P(x > 950) = 1 - 0.952 = 0.048`

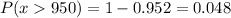
0.048 is the probability that more than 950 message arrive in one minute.