Answer:
a) There is a 45% probability that the individual must stop at at least one light.
b) 55% probability that the individual needn't stop at either light.
c) 30% probability that the individual must stop at exactly one of the two lights.
d) 25% probability that the individual must stop just at the first light.
Explanation:
The problem says that:
P(E) is the probability that a person has to stop at the first light.
P(F) is the probability that a person has to stop at the second light.
We have that:
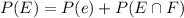
In which P(e) is the probability that a person has to stop at the first light but not the second and
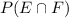 is the probability that a person has to stop at both these lights
is the probability that a person has to stop at both these lights
By the same logic, we have that:
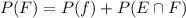
Lets find each value:
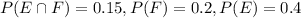
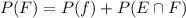
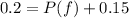

---------
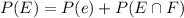
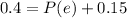
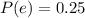
(a) What is the probability that the individual must stop at at least one light; that is, what is the probability of the event P(E union F)?
This is
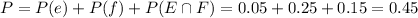
There is a 45% probability that the individual must stop at at least one light.
(b) What is the probability that the individual needn't stop at either light?
Either a person has to stop in at least one light, or the person does not have to stop at any.
The sum of these probabilities is decimal 1. So this probability is 1 subtracted by the probability found in a).
So 1-0.45 = 0.55 = 55% probability that the individual needn't stop at either light.
(c) What is the probability that the individual must stop at exactly one of the two lights?
This is P(e) + P(f) = 0.25 + 0.05 = 0.30 = 30% probability that the individual must stop at exactly one of the two lights.
(d) What is the probability that the individual must stop just at the first light?
This is P(e) = 0.25.
So there is a 25% probability that the individual must stop just at the first light.