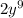Question

Match The exponential expression on the left with the equivalent simplified expression on the right?

Answer 1

Image for the above Question is Missing hence Attached below.

`y^(2)y^(4)` ⇒
`y^(6)`

`(2y)^(2)` ⇒
`4y^(2)`

`((y)/(4))^(2)` ⇒
`(y^(2))/(16)`

`2((y)^(3))^(3)` ⇒
`2y^(9)`

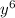
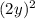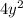
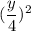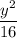
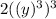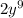
Explanation:

We have Law of Indices as follow

1.
`x^(a)x^(b)=x^(a+b)`

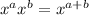
2.
`(xy)^(a)=x^(a)y^(a)`

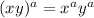
3.
`((x)/(y))^(a)=(x^(a))/(y^(a))`

4.
`((x)^(a))^(b)=x^(a* b)`

Using above identities we get

For First

`y^(2)y^(4)=y^(2+4)=y^(4)`

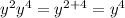
Therefore
`y^(2)y^(4)` ⇒
`y^(6)`

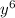
For Second

`(2y)^(2)=2^(2)y^(2)=4y^(2)`

Therefore
`(2y)^(2)` ⇒
`4y^(2)`

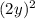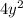
For Third

`((y)/(4))^(2)=(y^(2))/(4^(2))=(y^(2))/(16)`

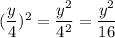
Therefore
`((y)/(4))^(2)` ⇒
`(y^(2))/(16)`

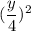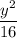
For Fourth

`2((y)^(3))^(3)=2y^(3* 3)=2y^(9)`

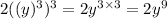
Therefore
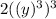`2((y)^(3))^(3)` ⇒
`2y^(9)`