Question

Use the concept of volume to explain why the determinant of a 3×3 matrix A is zero if and only if A is not invertible. What must be done to prove that the determinant of a 3×3 matrix A is zero if and only if A is not​ invertible?

Answer 1

See explanation below

Explanation:

On this case what we need to proof is:

"If the matrix A is not invertible then the determinant is 0"

Let A the matrix of interest. If the matrix is not invertible then
`det (A) =0`

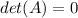
Let denote the inverse of A as
`A^(-1)`

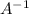
If the matrix is not invertible we have this:

`A A^(-1) =A^(-1)A \\eq I`

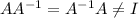
And taking determinant in both sides we get:

`det(AA^(-1)) \\eq det I`

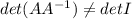
And using propoerties of determinants we got:

`det A det A^(-1)\\eq 1`

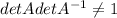
A 3x3 matrix A is not invertible if and only if its columns are linearly independent.

And if the columns are linearly indpendent then the determinant is 0. And we can associate this to the volume with the following theorem

"Let v 1 , v 2 ,..., v n be vectors in R n , let P be the parallelepiped determined by these vectors, and let A be the matrix with rows v 1 , v 2 ,..., v n . Then the absolute value of the determinant of A is the volume of P."

And if one vector is linear dependnet we have that the detemrinant would be 0 and the matrix would not invertible