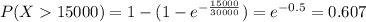Answer:
a)
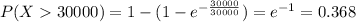
b)
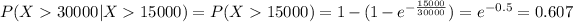
Explanation:
Previous concepts
The exponential distribution is "the probability distribution of the time between events in a Poisson process (a process in which events occur continuously and independently at a constant average rate). It is a particular case of the gamma distribution". The probability density function is given by:
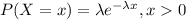
And 0 for other case. Let X the random variable that represent "life lengths of automobile tires of a certain brand" and we know that the distribution is given by:
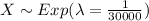
The cumulative distribution function is given by:
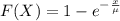
Part a
We want to find this probability:
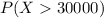 and for this case we can use the cumulative distribution function to find it like this:
and for this case we can use the cumulative distribution function to find it like this:
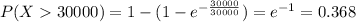
Part b
For this case w want to find this probability
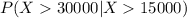
We have an important property on the exponential distribution called "Memoryless" property and says this:
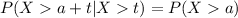
On this case if we use this property we have this:
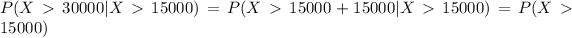
We can use the definition of the density function and find this probability: