Question

Consider the function f ( x ) = − 2 x 3 + 27 x 2 − 108 x + 9 . For this function there are three important open intervals: ( − [infinity] , A ) , ( A , B ) , and ( B , [infinity] ) where A and B are the critical numbers. Find A and B

Answer 1

A=3 and B=6

Explanation:

Increasing and Decreasing Intervals of Functions

Given f(x) as a real function and f'(x) its first derivative.

If f'(a)>0 the function is increasing in x=a

If f'(a)<0 the function is decreasing in x=a

If f'(a)=0 the function has a critical point in x=a

As we can see, the critical points may define open intervals where the function has different behaviors.

We have

`f ( x ) = - 2 x^3 + 27 x^2 - 108 x + 9`

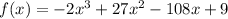
Computing the first derivative:

`f' ( x ) = - 6 x^3 + 54 x - 108`

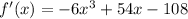
We find the critical points equating f'(x) to zero

`- 6 x^3 + 54 x - 108=0`

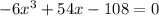
Simplifying by -6

`x^2 -9 x +18=0`

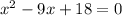
We get the critical points

`x=3,\ x=6`

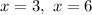
They define the following intervals

`(-\infty,3),\ (3,6),\ (6,+\infty)`

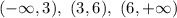
Thus A=3 and B=6