Question

You are working for a renowned head hunting company in midtown Manhattan. Your job is to identify high potentials for the financial services industry. The prior probability that someone you will consider is a high potential is 0.03. If someone is a high potential, their probability of having a degree from an Ivy League school is 0.6 and the probability that they have an Ivy League degree if they are not a high potential is 0.05. The person you are considering has an Ivy League degree. What is the probability that they are a high potential?A. 0.03 B. 0.27 C. 0.33 D. 0 E. 0.66

Answer 1

B. 0.27

Explanation:

We have these following probabilities:

A 3% probability you will consider someone with high potential.

A 97% probability that you consider someone who does not have high potential.

If a person has high potential, there is a 60% probability that she has an Ivy League degree.

If a person does not have high potential, there is a 5% probability that she has an Ivy League degree.

This can be formulated as the following problem:

What is the probability of B happening, knowing that A has happened.

It can be calculated by the following formula

`P = (P(B).P(A/B))/(P(A))`

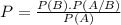
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

In this problem, we have that:

What is the probability that a person has high potential, given that they have a Ivy League degree?

P(B) is the probability that a person has high potential. So P(B) = 0.03.

P(A/B) is the probability that a person has an Ivy League degree, given that she has high potential. So P(A/B) = 0.6.

P(A) is the probability that a person has an Ivy League degree. It is 0.6 of 0.03 and 0.05 of 0.97. So

`P(A) = 0.6*0.03 + 0.05*0.97 = 0.0665`

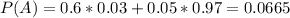
What is the probability that they are a high potential?

`P = (P(B).P(A/B))/(P(A)) = (0.03*0.6)/(0.0665) = 0.27`

The correct answer is:

B. 0.27