Answer:
horizontal distance on moon > horizontal distance on earth
Step-by-step explanation:
Let the time of fall is t and the height from which they fall is h.
The time of fall is
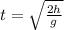
Time of fall on earth
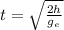
Time of fall on moon

As the gravity on moon is less than the gravity on earth
So, t' > t
Horizontal distance = horizontal velocity x time
So, the horizontal distance on moon is more than the horizontal distance on earth.